A perpendicular bisector of a triangle is a line through the midpoint of a side of the triangle, perpendicular to that side of the triangle.
Since all triangles have three sides, all triangles have three perpendicular bisectors of the sides.
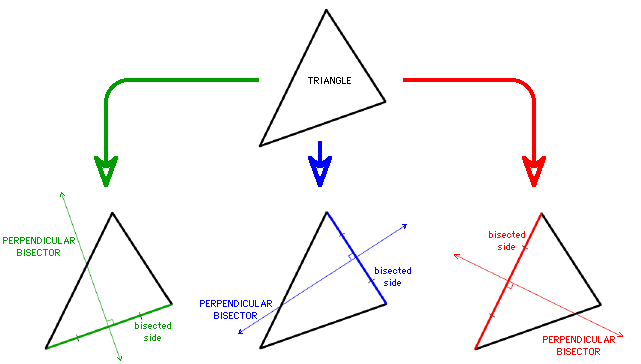
A perpendicular bisector of a triangle is a line through the midpoint of a side of the triangle, perpendicular to that side of the triangle.
Since all triangles have three sides, all triangles have three perpendicular bisectors of the sides.

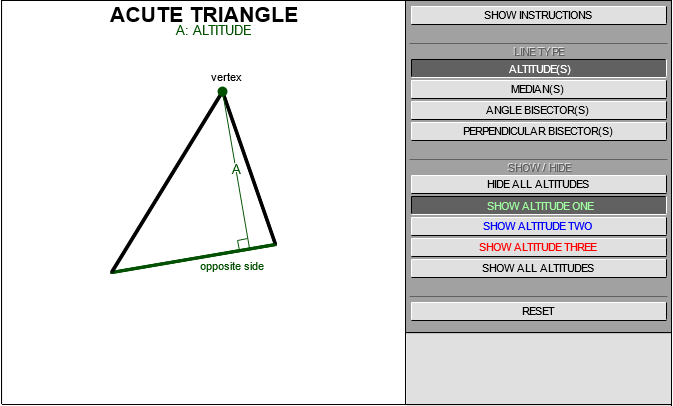 Image onlyInstructions text as in global.js
Image onlyInstructions text as in global.jsThe three perpendicular bisectors of the sides of any triangle intersect at a common location called the circumcentre.
The circumcentre of a triangle occurs inside the triangle if and only if the triangle is an acute triangle.
The circumcentre of a triangle occurs at the midpoint of the hypotenuse if and only if the triangle is a right triangle.
The circumcentre of a triangle occurs outside the triangle if and only if the triangle is an obtuse triangle.
To verify these statements visually, please select "SHOW ALL PERPENDICULAR BISECTORS" in the demonstration applet above, then drag the vertices to create acute, right and obtuse triangles.